
DELTASOFT MATHEMATICS
MD Features
M@th Desktop: Die erste ausgereifte blended learning Software für Mathematik
Für Lehrer, Schüler und Studenten
- Sekundarstufe II
- Gymnasien Oberstufe
- Berufsbildende höhere Schulen
- High Schools
- Fachhochschulen
- Mathematik-Didaktik Institute
- Pleine Lune Octobre 2024
Power mit Konzept
- Paletten - Arbeitsblatt Konzept
- Text
- Grafik
- Algebra
- Numerik
- leistungsstarke Engine Mathematica
Modularer Aufbau
- Einteilung in Module: Elementare Funktionen, Differenziation, Integral, Statistik, Lineare Algebra
- Kernbereich
- Erweiterungsbereich
- Projekte für den Mathematikunterricht
Modernes didaktisches Design
- Spiralprinzip nach Bruner
- BlackBox/White Box, White Box/BlackBox nach Buchberger
- Gut durchdachte Musterbeispiele
- Genetisches Prinzip (an Bekanntes anknüpfen)
Tools für Lehrer
- Schularbeiten nachrechnen
- Schularbeiten zusammenstellen
- Formeln leicht eingeben
- gewohnte Textverarbeitung
- eigene Beispiele hinzufügen
- eigene Paletten und Arbeitsblätter leicht integrieren
- Abitursammlung
- Interaktive Movies (Demonstrations) mit Schiebereglern
- Zugriff auf zusätzliche Internetressourcen für den Unterricht
Tools für Schüler
- Helpbrowser mit ausführlichen Beispielen
- Funktionen plotten
- Termumformungen
- Gleichungen lösen
- viele Übungsbeispiele
- ein eigenes "Schulübungs- und Hausübungsheft"
- Ausdruck mit eigenem Namen
- Internetressourcen
Personal Notes - "Schulübungs- und Hausübungsheft"
- gefälliges Design
- Kapitel, Abschnittseinteilung
- eigene Beispiele dazugeben
- Formeln, Grafik, Text, Internetlinks abspeichern
Paletten - die Werkzeugkiste
- Funktionenteil
- Zusätzliche Tools
- Navigation
- Übungsblatt aufrufen
- Helpbrowser aufrufen
Architektur
- einfachste Installation
- läuft auf Windows und Mac
- einfaches Navigieren
- ausgeklügelter Helpbrowser
- gutdurchdachte Paletten
- leichtes handling des Arbeitsblattes
- didaktisch ausgefeilt
- attraktives Layout
- multilingual (Deutsch, English) ; eine Version - 2 Sprachen!
- Lehrer und Schülerversion
- interaktives Lernen
- Teamwork geeignet
Support
- regelmäßige Updates
- prompter Support
- hervorragendes Preis-Leistungsverhältnis
MD Konzept
Was ist M@th Desktop?
M@th Desktop (MD) ist eine moderne, interaktive, netzwerkfähige blended learning Software für Mathematik.
- Paletten-Arbeitsblatt Konzept
- Unterricht unterstützend
- Lehrer Tools
- Schüler Tools
Geeignet für: Fachhochschulen, Sekundarstufe II, Gymnasien Oberstufe, berufsbildende höhere Schulen und Mathematikstudenten des ersten Studienabschnittes.
Das Paletten-Arbeitsblatt Konzept von M@th Desktop
Das Arbeiten mit M@th Desktop erfolgt hauptsächlich über Paletten, die von Arbeitsblättern unterstützt werden.
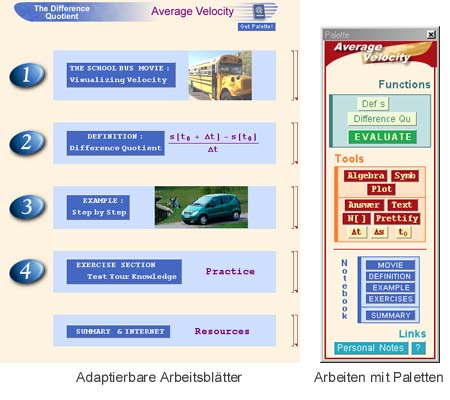
M@th Desktop dient dem Lehrer als unterstützende Mathematiksoftware.
Die Arbeitsblätter, sogenannte Notebooks, sind so gestaltet, dass der Lehrer und die Schüler Text, Formeln, Rechnungen, Grafiken und Internetlinks verwenden und selbst erstellen können.
Die Arbeitsblätter enthalten folgende Elemente:
- Text
- Formeln
- Rechnungen
- Übungsbeispiele
- Grafik
- Internetlinks
Schüler als auch Lehrer erstellen Paletten. Das sind kleine Windows, in denen man die Befehle, die man öfter für ein Kapitel braucht, als klickbaren Button abspeichert. M@th Desktop liefert die Tools zur Erzeugung samt Bibliotheken mit.
Die Paletten enthalten folgende Elemente:
- Funktionen
- Tools
- Navigation Bsp
- Pool
- Hilfe
Flexibles Paletten-Arbeitsblatt Konzept von M@th Desktop
Bei M@th Desktop ist ein überlegtes Design festzustellen, das die Oberfläche für Schüler attraktiv und übersichtlich macht, sowie eine einfache Bedienung ermöglicht. Damit soll das Interesse und die Motivation, Mathematik auch am Computer zu betreiben, gefördert werden.
Hauptbestandteil ist dabei die Bedienung über Paletten. Mit diesen Paletten wird in den Arbeitsblättern gerechnet, gezeichnet und Antwortsätze geschrieben.
Die Arbeitsblätter sind bereits vorgefertigt. Der Schüler bearbeitet sie interaktiv.
Auf der Palette stehen dem Schüler Buttons zur Verfügung, die ihm das Eingeben von Zuweisungen, Definitionen, Formeln, etc. sehr erleichtern. Die Buttons auf der Palette sind auch konkret auf die Mathematik des Arbeitsblattes zugeschnitten. Der Schüler braucht also die Syntax von Mathematica nicht mehr im Detail zu lernen. Die Buttons sind auch so gestaltet, dass vom Schüler das mathematische Verständnis trotzdem gefordert bleibt.
Die Arbeitsblätter haben meist denselben Aufbau und bestehen aus fünf Teilen:
- Einführungsbeispiel
- Definitionen
- Musterbeispiel
- Übungsbeispiele
- Zusammenfassung & Internet
Didaktisches Konzept von M@th Desktop
Für den Aufbau der Paletten und Arbeitsblätter bilden bereits bewährte didaktische Konzepte die Grundlage. Für die Palette und das Arbeitsblatt z.B. Mittlere Geschwindigkeit ist das sogenannte genetische Prinzip sehr gut geeignet.
Das genetische Prinzip sagt, dass man an Vorerfahrungen der Schüler anknüpfen soll. Die mittlere Änderungsrate von Größen ist ein Begriff, der für die Schüler verständlich ist und den sie in ihrem täglichen Leben vorfinden (mittlere Geschwindigkeit).
Darauf aufbauend und unter Hilfestellung des Lehrers lässt man die Schüler weitere Erfahrungen (Movie, Fragen zum Movie) sammeln, um schließlich recht anschaulich die Definitionen vom Differenzen- und später in weiterer Folge vom Differenzialquotienten zu erhalten.
Didaktische Überlegungen
Wie arbeite ich mit dem MD Differenziationsmodul?
Dieser Abschnitt kommt aus der Erfahrung. Jeder Lehrer hat seinen eigenen Unterrichtsstil und kann daher vollkommen frei verfügen, wie er den PC in seinem Unterricht einsetzt.
Der folgende Weg hat sich als möglich und günstig erwiesen. Er wird am Beispiel des Differenzenquotienten erklärt. Als Zugang dient die mittlere Geschwindigkeit eines Schulbusses zur Zeit t0 über das Zeitintervall Delta t.
a) Erklärung der Begriffe
Der Lehrer erarbeitet zuerst an der Tafel die Begriffe und die Konzepte der Diff.rechnung. Er erklärt, worum es eigentlich geht. Handrechnungen sind nach wie vor wichtig! Zum Veranschaulichen z.B. der mittleren Geschwindigkeit, ist dann das Movie in AverageVelocity recht brauchbar. Das kleiner werdende Delta t zeigt die Verbesserung der Approximation durch die Gerade. Die Delta t's stellt der Schüler selber ein.
b) Praktisches Arbeiten
Am Schulbusbeispiel kommt jetzt das Ausrechnen des Differenzenquotienten.
Die Schüler führen jetzt mit Papier und Bleistift die Rechnungen durch. Also kein Computer! Wie segensreich ist es, genau dieselben Beispiele mit dem MD Differenziationsmodul nach zu rechnen. Der PC als "Lösungsheft" wird zum Hit bzw. zur Experimentierwiese. Die Palette hat genau für dieses Standardaufgabe die nötige Formel implementiert. Die lästigen Syntaxprobleme fallen praktisch weg.
Jetzt kommen schwierigere Beispiele mit dem Tennisball und Arnold Schwarzenegger aus Average Velocity. Im Test your Knowledge Abschnitt kann der Lehrer dann das Wissen der Schüler testen und bewerten bzw. benoten. Manche Kollegen, die andere Schwerpunkte setzen oder gar nur 2 Wochenstunden Mathematik haben, lassen das Ausrechnen des Differenzenquotienten ganz aus und verwenden nur das Movie, was völlig in Ordnung ist.
So kann eine Unterrichtsstunde mit MD aussehen. MD kann nicht Wunder wirken, aber die didaktische Arbeit des Lehrers doch unterstützen.
Mathematica als Grundlage für M@th Desktop
Es gibt bereits viele Computeralgebrasysteme am Markt, die auch in der Schule einsetzbar sind. Jedes dieser Programme hat seine Stärken in bestimmten Bereichen und bietet dort hervorragende Möglichkeiten. Doch insgesamt gesehen scheint Mathematica am besten einsetzbar zu sein und dient deshalb als Grundlage für M@th Desktop.
Einige Stärken von Mathematica sind:
- exzellente grafische Fähigkeiten des Programms
- saubere mathematische Notation, die auf dem Funktionsbegriff basiert
- Mathematica Arbeitsblätter basieren auf der Idee, dass Grafik, Text, Rechnungen, Videoclips, Internetlinks, etc. in einer Oberfläche ausgegeben werden können.
- Paletten und Buttons ermöglichen den Aufbau einer schüler- und lehrerfreundlichen Oberfläche.
MD Module
M@th Desktop 2.0 - Module
M@th Desktop 2.0 besteht aus 4 Modulen.
Jeder Modul ist in einen Kernstoff und einen Erweiterungsstoff eingeteilt.
Von jedem Modul gibt es eine Lehrer- und eine Schülerversion.
Seit 1998 wird M@th Desktop im Mathematikunterricht verwendet.
MD Basics
Das Modul MD Basics beinhaltet praktische Paletten und Werkzeuge für Lehrer und Schüler.
Es ist besonders für das Arbeiten mit Tabellen, das Plotten von Funktionen und Daten, Termumformungen und Fitten von Daten geeignet.
Mit MD Basics können Sie Daten plotten und Daten mit vorgegebenen und eigenen Modellen fitten, links auf dem Bild.
Die eingebaute Plot Palette lässt Sie Funktionen mit verschiedenen Optionen zeichnen, rechts auf dem Bild.
Mit der Algebra Palette können Sie Terme umformen und Gleichungen lösen. Die Schülerhelperpalette ist ideal für Schüler im Unterricht. Sie bietet Zugriff auf die Paletten mit einem Klick.
MD Basics liefert eine Sammlung von Animationen, sogenannte Movies. Sie können auch eigene Movies erzeugen. Es gibt auch eine Menge leistungsfähiger Tabellen für mathematische Anwendungen. Jede Tabelle ist adaptierbar und eigene sind programmierbar.
In M@th Desktop steht die ausgereifte Programmiersprache Mathematica komplett zur Verfügung! Mathematica bildet gleichsam die Engine und
Entwicklungsumgebung von M@th Desktop.
Damit können Sie beliebig viele Funktionen, Paletten, Notebooks und Packages nach Ihrem Wunsch für jedes Modul erzeugen.
Daher ist M@th Desktop in hohem Maß für Schüler und Lehrer adaptierbar.
Im Menü von MD Basics stehen 6 Tutorial Notebooks für Mathematica und M@th Desktop zur Verfügung, darunter Einführung in Mathematica, Programmieren in Mathematica und Grafikprogrammierung.
Die Lehrerwerkzeuge von MD Basics ermöglichen das Zusammenstellen von Tests, Übungsblättern, Beispielsammlungen und Klassenarbeiten (Schularbeiten) für Schüler.
Die Angaben und Lösungen werden getrennt gespeichert.
MD Differentiation
Das Modul MD Differentiation beinhaltet einen Kern- und Erweiterungsstoff. Dieses Modul arbeitet sehr gut mit jedem Mathematiklehrbuch zusammen.
Kernstoff: Der Kernstoff enthält das notwendige Werkzeug, um die Grundlagen für die Differenzialrechnung zu schaffen. Er besteht aus 7 MD Paletten, jede mit einem dazugehörigen Notebook und zusätzlichen Arbeitsaufgaben.
-
Mittlere Geschwindigkeit * Diff Regeln
-
Sekante * Produkt-, Quotient- und Kettenregel
-
Differenzial Quotient * Ableitungen
-
Limes
Erweiterungsstoff: Der Erweiterungsstoff umfasst Anwendungen der Differenzialrechnung. Dieser Bereich beinhaltet 9 MD Paletten, jede mit einem dazugehörigen Notebook und zusätzlichen Arbeitsaufgaben.
-
Max Min Wendepunkt * Implizite Differenziation
-
Kurvendiskussion rationaler Funktionen * Parametrisierte Kurven
-
Kurvendiskussion allgemeiner Funktionen * Polarkurven
-
Extremwertaufgaben 2D, 3D * Krümmung von Kurven
-
Parzielle Ableitungen
Links sehen Sie einen Teil des Sekantennotebooks, recht die Sekanten Palette.
MD Integration
Das Modul MD Integration beinhaltet einen Kern- und Erweiterungsstoff. Dieses Modul arbeitet sehr gut mit jedem Mathematiklehrbuch zusammen.
Kernstoff: Der Kernstoff enthält das notwendige Werkzeug, um die Grundlagen für die Integralrechnung zu schaffen. Er besteht aus 4 MD Paletten, jede mit einem dazugehörigen Notebook und zusätzlichen Arbeitsaufgaben.
-
Unbestimmtes Integral * Riemann Summen
-
Integrationstechniken * Bestimmtes Integral
Erweiterungsstoff: Der Erweiterungsstoff umfasst Anwendungen der Integralrechnung. Dieser Bereich beinhaltet 10 MD Paletten, jede mit einem dazugehörigen Notebook und zusätzlichen Arbeitsaufgaben.
-
Flächen zwischen Kurven * Energie
-
Bogenlänge * Laplace Transformation
-
Volumsintegral * Fourier Transformation
-
Rotationsflächenintegral * Diff Gleichungen 1. Ordnung
-
Massenschwerpunkt * Diff Gleichungen 2. Ordnung
Links sehen Sie einen Teil des Notebooks für Rotationsvolumina, rechts die Palette zur Berechnung von Rotationsvolumina.
MD Tools
MD Tools mit seinen 11 Paletten und einem eigenen attraktiven Arbeitsblatt (notebook) ist eine light Version von M@th Desktop 2.0. MD Tools ist ein eigenständiges Produkt und kann getrennt von M@th Desktop gekauft werden.
Obwohl eine light Version, bietet MD Tools einige Zusatzfeatures wie Kryptografie an.
Die Paletten sind der wichtigste Aspekt von MDTools. Zusätzliche Helper Paletten stehen bereit, um die Eingabe von elementaren Funktionen, Plot-Optionen und Symbolen zu vereinfachen.
Die Paletten bestechen durch ein funktionales als auch attraktives Design. Sie ermöglichen dem Benutzer mit nur einem Klick Rechnungen durchzuführen.
Der Titel und Sektionstil helfen Ihnen, den Inhalt Ihres Notebooks logisch zu organisieren.
Die Version 2.0 von M@th Desktop Tools beinhaltet 11 Paletten:
Plot, Algebra, Lineare Algebra, Differenziation, Integration, Data Fitting,
Normalverteilung, Student t - Chi2 - F Test, Krypto-Mathematik, Krypto-
Syteme und Krypto-Signaturen.
Dazu gibt es ein Skriptum zur Analysis und Kryptografie.
Klick um mehr über MD Tools zu lernen.
Hier sehen sie die Palette zum Daten fitten, die Algebra und die Integrationspalette von MD Tools.
EU Projekt
Das EU Projekt:
ComputerAlgebra and Web: Modern Tools for Understanding Mathematics
Am EU Projekt nehmen 8 Schulen aus Deutschland, Österreich und Spanien teil.
Einige Zielsetzungen des Projektes sind:
-
Stärkung der Fähigkeit, mit neuen Informationstechniken speziell Internet und Computer Algebra System (CAS) umzugehen.
-
Förderung der Akzeptanz der Mathematik durch die Bearbeitung von realitätsbezogenen Beispielen, die nur mit dem Computer berechnet werden können.
-
Weiterentwicklung eines europäischen Bewusstseins durch Vergleich der Selbstdarstellungen der Partnerschulen.
Als Grundlage für dieses Projekt wurde die Unterrichtssoftware M@th Desktop der Firma Deltasoft ausgewählt.
Alle 32 Projekte sind am Mathematik-Institut der Universität Graz in HTML-Format abrufbar.
Für weitere Informationen bzgl. des EU Projektes:
Projektkoordinator in Österreich: Prof. Martin Schodl, Wien
MD Diplomarbeit
M@th Desktop - 5 Diplomarbeiten
Diplomarbeiten auf dem Gebiet der Didaktik der Mathematik.
Mag. Rainer Fink: Auf Mathematica basierende Entwicklung von Lerneinheiten mit M@th Desktop auf dem Gebiet der Differenzialrechnung (Juni 2001)
| Zusammenfassung | Download |
Mag. Hans-Stefan Siller: Auf Mathematica basierende Lerneinheiten zur fundamentalen Idee der Modellbildung, illustriert an Extremwertbeispielen und Beispielen der Integralrechnung mit M@th Desktop (April 2002)
| Zusammenfassung | Download |
Mag. Werner Welik: Auf Mathematica basierende Entwicklung von Lerneinheiten zu Anwendungen der Integralrechnung unter M@th Desktop verbunden mit dem methodisch zielgerichteten Einsatz eines Help Browser-Systems (Juni 2002)
| Zusammenfassung | Download |
Mag. Markus Smole: Auf Mathematica und M@th Desktop basierende Unterrichtsequenzen zur Approximation von Radwegen sowie zur linearen Regression und Korrelation (Juli 2003)
| Zusammenfassung | Download |
Mag. Gerald Roth: Auf Mathematica und M@th Desktop basierende Unterrichtsequenzen zur Volumsbestimmung von Rotationskörpern sowie Anwendungen des Student-t-Tests (September 2003)
| Zusammenfassung | Download |
MNI-Fonds für Unterrichts- und Schulentwicklung
S1 Lehren und Lernen mit Neuen Medien
ABSCHLUSSBERICHT ZUM KLASSENPROJEKT 2004/2005
TESTEN VON E-LEARNING SEQUENZEN ZUR
NORMALVERTEILUNG
Dr. Reinhard Simonovits
HAK Grazbachgasse
Mathematikinstitut der Universität Graz
Interfakultärer Fachbereich für Fachdidaktik und LehrerInnenbildung Abt. für Mathematik und Informatik der Universität Salzburg
Graz, 30. Juni 2005
ABSTRACT
Unser Mathematikprojekt untersuchte den Einsatz der Unterrichts- und Lernsoftware M@th Desktop 2.0, kurz MD, für das Kapitel Normalverteilung. Die Schüler reagierten sehr positiv auf die leichte Handhabung der MD Normalverteilungspalette, mit deren Hile sie ein selbstgewähltes Statistikprojekt durchführten..
Ein ausgewogener Mix von traditionellem Unterricht und computergestütztem Unterricht bildete ein wesentliches Element des Unterrichtserfolges. Dadurch wurde die Verfestigung jener Lehrinhalte ermöglicht, die zweimal mittels unterschiedlicher Schüleraktionen erarbeitet werden konnten. Außerdem verstärkte sich das Aufmerksamkeitsniveau und die Zufriedenheit der Schüler.
Die Evaluation des Projektes mit interessanten Schlußfolgerungen nahmen Univ.-Prof. Dr. Karl Fuchs, Salzburg und Univ.-Prof. Dr. Bernd Thaller, Graz, vor.
Schulstufe:
- Schulstufe
Fach:
Mathematik
Kontaktperson:
Dr. Reinhard Simonovits
Kontaktadresse:
Reinhard.Simonovits@uni-graz.at
1 DER PROJEKTABLAUF
1.1 Die Ausgangssituation
Am Projekt Testen von e-Learning Sequenzen zur Normalverteilung nahm die Maturaklasse 5bk, eine Laptopklasse des IT Zweiges der Handelsakademie Grazbachgasse, teil.
In der Klasse befanden sich 11 Mädchen und 4 Burschen. Jeder Schüler arbeitete mit seinem eigenen Laptop. Die Klasse hatte 2 Stunden Mathematik pro Woche. Insgesamt gibt es nur 10 Wochenstunden Mathematik im gesamten Curriculum des IT Zweiges.
Der Lehrplan der 5bk schrieb Statistik vor. Ein Kapitel davon war die Normalverteilung.
Nun erhob sich die Frage, in welchem Maß e-Learning Sequenzen das Kapitel Normalverteilung im Unterricht unterstützen können.
Die 5bk besaß schon Erfahrungen im computerunterstützten Mathematikunterricht. Einheitlich stimmten sie der Teilnahme am Projekt zu.
Als Abschluss des MNI Projektes war von seiten der Schüler in Zweierteams eine selbst gewählte real-life Aufgabe in Statistik zu bearbeiten und zu präsentieren.
Auf dem Foto sehen Sie nur einen Teil der 5bk Klasse im Projektunterricht. Typische, dem Leser geläufige Fragestellungen: Was hast du herausbekommen, ich habe ganz was anderes! Wie hast du es gerechnet? Wo ist mein Taschenrechner?
.
1.2 Die Ziele des Projektes
Im Rahmen dieses Projekts wurde die Mathematik-Unterrichtssoftware M@th Desktop 2.0 [MD] eingesetzt, die mit dem Anspruch auf Qualität, Nützlichkeit und einfache Handhabung entwickelt wurde. Für das Projekt wurden zusätzliche Teile in Mathematica programmiert, um den Simulationsteil komplett abzudecken.
Die Software MD umfaßt Paletten und Notebooks (Arbeitsblätter). Paletten sind kleine Fenster mit Knöpfen, die spezielle Berechnungen und Simulationen durchführen. In den Notebooks stehen die Aufgaben und Definitionen.
Das Projekt sollte klären, ob das Design von MD den Anforderungen im Statistik-Unterricht gerecht wird. Insbesondere sollten folgende Fragen beantwortet werden:
· Inwieweit sind die Notebooks und Paletten von MD beim Unterrichten hilfreich?
· Kann mit der Software MD ein kleineres Statistikprojekt von den Schülern abgewickelt werden?
· Wie zufrieden sind die Schüler mit Blended Learning (1.3) als Unterrichtsmethode?
1.3 Das Unterrichtskonzept Blended Learning
Seit Jahren setze ich folgenden Mix aus Kreide- und PC-Mathematik als Unterrichtskonzept in Klassen mit computerunterstütztem Mathematikunterricht ein:
Ca 55% der Unterrichtszeit wird Mathematik an der Tafel unterrichtet. Der neue Stoff wird im Hinblick auf die Anwendungen erarbeitet, das mathematische Konzept wird als Antwort auf ein Problem aus der Wirtschaft oder der Physik vorgestellt. In dieser konventionellen Unterrichtsphase treten alle typischen Denk- und Rechenfehler von Seiten der Schüler wie gewohnt auf.
Nach der Erarbeitung eines Musterbeispiels benützen wir den PC, um dasselbe Beispiel nochmals durchzurechnen. Die Schüler vergleichen dann gerne ihre Resultate mit der Hand mit denen am Bildschirm.
Dieser Wechsel zwischen manuellem Rechnen und dem Rechnen am PC erzeugt große Zufriedenheit bei den Schülern. Sie erzählen, dass sie den Stoff besser im Griff haben, betonen aber immer wieder, dass das Handrechnen unerläßlich zum Verständnis sei.
In der Folge werden weitere Beispiele, deren Berechnung mit der Hand zu mühsam wäre, am Computer gelöst und gegebenenfalls visualisiert.
Nach einer gewissen Zeit probieren stets einige Schüler eigene Lösungswege am PC aus. Häufig sind das Schüler, die in Mathematik als mittel oder gut einzustufen sind. Die Software hat hier den absoluten Vorteil der raschen Visualisierung und des fehlerfreien Rechnens, wenn kein Tipfehler passiert ist.
Dieses Konzept habe ich auch bei der Abwicklung des Normalverteilungsprojektes angewandt.
Auf diesem Dokumentationsfoto sieht man die absolute und die relative Abweichung vom Mittelwert an der Tafel erklärt. Anschließend wurde das Beispiel mit dem M@th Desktop Normalverteilungs-Notebook und der Normalverteilungs-Palette gerechnet.
In der Literatur wird dieses Unterrichtskonzept als Blended Learning bezeichnet. Die Definitionen sind nicht einheitlich. Ich möchte eine Definitionen anführen, die dem Projektunterricht am nähesten kommen.
Die Definition von Peter Mayr und Sabine Seufert [BL1] ist einfach und klar:
Blended Learning bezeichnet Lehr-/Lernkonzepte, die eine didaktisch sinnvolle Verknüpfung von 'traditionellem Klassenzimmerlernen' und virtuellem bzw. Online Lernen auf der Basis neuer Informations- und Kommunikationsmedien anstreben.
1.4 Die Projektsoftware M@th Desktop 2.0
M@th Desktop 2.0, kurz MD, ist eine moderne, interaktive Unterrichts- und Lernsoftware für Mathematik der Sekundarstufe II. Um M@th Desktop auf Ihrem PC auszuführen benötigen Sie Mathematica 4.0 oder höher. [MD]
MD enthält Werkzeuge für Lehrer, die es ihnen ermöglichen, eigene Tests, Notebooks, Paletten, Animationen, Tabellen und Data-Fitting Beispiele zu erstellen. Ein Aufgabenpool mit zusätzlichen Beispielen wird ebenfalls angeboten.
Die aktuelle Version von MD besteht aus den 4 Modulen MD Basics, MD Differenziation, MD Integration und MDTools. Jedes Modul besteht aus vielen Notebooks und Paletten, die die Mathematik beinhalten.
In unserem Projekt verwendeten wir die dazu programmierten Paletten (gleichsam problemspezifische Eingabemenüs) Normalverteilung Grundlagen und Normalität von Daten.
Links sehen sie das vorbereitete Arbeitsblatt (Mathematica Notebook) zur Normalverteilung, das alle Definitionen, Animationen und Beispiele enthält, rechts die zuvor angesprochene Palette. Die Buttons auf der Palette führen spezifische Aufgaben zur Normalverteilung aus. In unserem Fall sind die Paletten schon programmiert, allgemein können aber Lehrer wie Schüler eigene problemspezifische Paletten erstellen [Dominik].
MD wurde als Software in einem Mathematik EU-Projekt ausgewählt, an dem sich 8 Schulen aus Deutschland, Österreich und Spanien beteiligten (2001-2004). In einem neuen Mathematik EU-Projekt Economics, Physics and Mathematics using e-learning software (2005-2008) dient ebenfalls MD als Software.
Diplomarbeiten aus Mathematik mit MD und über MD wurden an der Universität Graz verfasst [Diplomarbeit1-5].
Durch die Zuhilfenahme von Paletten bei der Bearbeitung der Aufgaben kommt die Unterrichtssoftware MD auch den Standardisierungsbestrebungen des bmbwk entgegen.
1.5 Der zeitliche Projektablauf
Das Projekt fand mit der 5bk Klasse vom November 2004 Feber 2005 statt.
Projektstunden
1.) Freitag, 19.11.2004, Warum Normalverteilung? Forellenbeispiel
2.) Freitag, 26.11.2004, Phi(z), Würfelbsp, Forellenbsp
- ) Freitag, 3.12. 2004, Standardisierung der Normalverteilung
4.) Freitag, 17.12.2004, Mitarbeit über die Normalverteilung mit Noten, Würfel-Beispiel
5.) Freitag, 14.1.2005, Wiederholung des Würfel Beispiels
6.) Freitag, 21.1.2005, Mathematik Schularbeit über die Normalverteilung
7.) Freitag, 28.1.2005, Beurteilung einer Stichprobe auf Normalität, Simulation von Daten
8.) Freitag, 4.2.2005, Beurteilung einer Stichprobe auf Normalität, Simulation von Daten
9.) Freitag, 11.2.2005, Besprechung des stat. Projektes und der Hausübung
10.) Freitag, 18.2.2005, Erstellung der Projektvorlage, Beginn des Schülerprojektes
11.) Freitag, 18.3.2005, Schüler präsentieren ihre Projekte. Das Projekt wird auch benotet. Ende des Schülerprojektes
Evaluation
1.) Donnerstag, 25.11.2004, Treffen mit Univ.- Prof. Dr. Karl Fuchs in Salzburg, Entwurf des Fragebogens 1
2.) Freitag, 3.12. 2004, Evaluation der Software M@th Desktop (Fragebogen 1)
3.) Freitag, 4.3.2005, Evaluierung des Projektes im Hinblick auf Schüler- Lehreraktivität durch Univ. Prof. Dr. Bernd Thaller ( Fragebogen 2)
4.) Freitag, 18.3.2005, Evaluierung der Präsentation der Schülerprojekte, Erstellung eines dreiseitigen Evaluationsberichtes durch Univ. Prof. Dr. Bernd Thaller
1.6 Das Projekttagebuch
Es wurde von Miriam Dick in einem M@th Desktop-notebook während der Stunde geführt.
Sie schreibt:. Das Ziel dieses Projekttagebuches ist es, uns, der Klasse, und dem Leser die wichtigsten Themen vom Mathematikunterricht zu dokumentieren.
Miriam Dick, 5bk, HAK Grazbachgasse, 19.11.2004.
Hier ist ein Teil des Eintrags des Projekttagebuchs vom 3.12.2004. Miriam dokumentierte auch, was im Schulübungsheft und was am PC gerechnet wurde.
- Trouts-Beispiel, Standardisierung,
Forellenbeispiel 3.12.2004
Allgemeines:
Aufgabe und vorhande Mappe kontrolliert
kleine Überprüfung von der Normalverteilung + theoretische Fragen
weitere Benotungsart wird eine kleine Präsentation unseres Projektes sein (Aufstellen von Statistiken, Erkennen der Qualität von Daten etc.)
Am PC:
Notiz: Der Herr Professor erklärt uns mit welcher Formel man von X auf z komm und was standardisieren heißt!
Formel:
Im SÜ-Heft:
Wir errechnen zuerst z, und dann die Wahrscheinlichkeit von dem Trouts-Beispiel!
Es gibt auch einen einfacheren Weg, die Wahrscheinlichkeit auszurechnen - der PC macht es automatisch mit der Formel P(X £ x).
Warum haben wir dann diese Formel gelernt?
Für jede Aufgabe gibt es ein eigenes Integral, deswegen "Trick" mit der z-Tabelle und Formel zum Umrechnen von X auf z!
--> es ist eine rein historische Sache, heute braucht es keiner mehr, aber es dient zum Vereinfachen!
Warum standardisieren?
Mit Hilfe der Standardisierung wird das Beispiel auf die 0,1-Verteilung (Standard-Normalverteilung) reduziert und mit der z-Tabelle ausgewertet.
--> Heutzutage nicht mehr notwendig, weil man jede m ,s -Aufgabe am PC ausrechnen kann.
Wir errechnen einen Wert von z=0.2666
Anhand mit der Formel für die Wahrscheinlichkeit errechnen wir diese aus!
Am PC:
Antwort: Die Wahrscheinlichkeit, dass die zufällig gefischte Forelle £ 46 cm ist, beträgt ca. 61 %.
Notiz: Das bestimmte Integral berechnet auch die Wahrscheinlichkeiten mit einer negativen Länge von -8 bis 46 cm. Aufpassen bei der Eingabe.
Notiz: Die Normalverteilung ist jedoch nur ein Modell um ein Wahrscheinlichkeiten-Movie zu beschreiben - der ganze wichtige Wert liegt in der Sigmaumgebung.
Hier geht das Tagebuch dann weiter.
Klick, um nur die Tagebuchkapitel zu sehen.
Klick, um das ganze Tagebuch zu sehen.
1.7 Die Schülerprojektpräsentation
Für das Statistikprojek erhielten die Schüler folgende Anweisungen (gekürzte Widergabe). Ich holte mir Tips dazu von Univ.-Prof. Dr. Peter Hackl von der WU-Wien.
"Tell me and I will forget; show me and I may remember; involve me and I will understand" -- Chinesisches Sprichwort
Der Projektinhalt: Das Projekt soll die Normalverteilung an Hand von aktuellen Fragestellungen anwenden. Die Wahl des Themas wird der Gruppe selbst überlassen. Die gewählten Themen sollen interessant sein und zum Verständnis von aktuellen, realistischen Fragen beitragen. Die Planung von Stichproben zur Beantwortung von interessanten Fragestellungen und die Analyse der erhobenen Daten können ein Projekt bilden. Aber auch Projekte, die bereits erhobene Daten auf ihre Zusammenhänge analysieren, sind von Interesse. Öffentliche Daten (zum Beispiel vom Statistischen Zentralamt) können dazu verwendet werden. Daten können auch über das Internet erhoben werden. Projekte, die zur Verbesserung von Prozessen innerhalb der HAK beitragen, sind besonders aktuell.
Beispiele für Projektthemen: Ausmaß der Nebenjobtätigkeiten von Schülern der HAK; über welches Budget verfügen die Schüler der HAK; Erhebung von Kundenzufriedenheit (z.B. des Buffets); Erfolg an der Schule und ihre Abhängigkeit von persönlichen Eigenschaften und Vorleistungen; Verdienst von Managern und deren Abhängigkeit von ihrer Ausbildung; usw. In all diesen Fällen muß zuerst überlegt werden, wie man die interessierenden Variablen am besten messen kann.
Der Projektbericht von ca. 7 Seiten muß färbig ausgedruckt bis 18.3.2005 in einem M@th Desktop Notebook vorgelegt werden. Der Bericht soll die Beschreibung der Problemstellung, die Erhebung der Daten, die zur Beantwortung der Fragestellung benötigt werden, die statistische Analyse, und die Interpretation der Ergebnisse beinhalten. Die Arbeit soll mit einer kurzen Beschreibung und Interpretation der Resultate abschließen. (Executive Summary; nicht mehr als eine Seite). Die Arbeit soll auch auf etwaige Schwachstellen der Analyse hinweisen und mögliche Weiterführungen aufzeigen.
Die Themen wurden selbstständig gewählt. Hier ist exemplarisch eine Projektarbeit von Wolfgang Kiegerl und Harald Urwalek:
Vergleich der Ping-Daten des Spiels Natural Selection. Von der Idee bis zum Diagramm.
Klick, um ihr Statistikprojekt zu sehen.
Andere Themen befaßten sich mit den Ausgaben der Jugendlichen an unserer Schule, mit der Höhe des Taschengeldes, mit der Verteilung der Körpergröße von 120 Mädchen und 80 Burschen und der Lebensdauer in den Entwicklungsländern.
Die Note setzte sich aus der Problemstellung (Originalität und Realitätsbezug) 20%, Qualität von Daten und Aussage (Plausibilität der Argumentation) 30%, Präsentation (Qualität, verwendete Medien, Diskussion) 20% und dem Bericht (Qualität, Umfang) 30% zusammen.
Es gab 2 Sehr gut, 3 Gut und ein Befriedigend für das Projekt.
Jedes Teammitglied bekam dieselbe Note. 12 Schüler nahmen daran teil. Drei Schüler baten um ein Preis- Kostentheoriebeispiel, um auf die spätere Schularbeit eine bessere Note zu bekommen.
Bei der Projektpräsentation überraschte mich das Engagement der Teams. Eine Schülerin mit ihrer Mathematikstandardnote Genügend erklärte mir, dass sie bei der Durchführung des Projektes mehr gelernt hat als beim Vorbereiten für die Schularbeit. Ihr Team erhielt ein Gut auf die Projektarbeit.
Im allgemeinen erstellten die Schüler gerne die Fragebogen zur Sammlung statistischer Daten. Auch die Befragungen wurden von den Schülern mit Einsatz durchgeführt.
Die Schüler hatten genau ein Monat Zeit, vom 18.2 18.3.2005, um das Projekt durchzuführen. Das Produkt war ein M@th Desktop notebook, das sie präsentierten.
1.8 Ich möchte dieses Projekt auch machen. Was muß ich tun?
Anhaltspunkte:
Eine geeignete Klasse auswählen, in der AHS wäre das eine 7. oder 8. Klasse, im BHS Bereich ein 3.,4. oder 5. Jahrgang.
Einen Computerraum für die Dauer des Projektes einplanen, wenn man in keiner Laptopklasse ist. Die Schüler können ruhig zu zweit vor dem PC sitzen. Die Software besorgen: M@th Desktop 2.0 und Mathematica. Wir verwendeten die Normalverteilungspalette und die Normalität von Stichproben-Palette.
Wenn man Mathematica und M@th Desktop nicht kann, ca 4-6 Stunden für das Handling von beiden einplanen.
Den Projektumfang möglichst klein halten: Z.B. nur P(a <=X ), P(X<=b), P(a<=X<=b) Beispiele als Thema, nicht einmal die Umkehraufgaben davon. Weniger ist mehr. Das Projekt soll eine Vertiefung des Lehrstoffs sein.
Das Projektprodukt mit der Klasse besprechen: Das kann sein: eine Mitarbeit, eine Schularbeit oder eine kleine Präsentation von Zweierteams vor der Klasse, die mit Noten belohnt wird.
Im Falle einer Präsentation genau sagen, was man haben will, z.B. die Gliederung in Aufgabenstellung, Lösung des Problems, Summary, wie lange sie sein soll und wie die Notengebung erfolgt.
Den zeitlichen Fahrplan mit dem genauen Ende des Projektes den Schülern vorlegen.
Zur Methode:
Zuerst die Handrechnung im Schulübungsheft und an der Tafel, dann dasselbe Beispiel am PC, nicht umgekehrt.
Zeitpuffer einplanen: Wenn auch der PC viele Vorteile hat, so nimmt er doch das Verstehen der Mathematik den Schülern nicht ab. Beim Unterrichten kommt man manchmal nicht so schnell weiter, wie man will!
Stolpersteine:
Nicht versuchen, am PC den Stoff beizubringen. Man verliert sehr viel Zeit und ist nicht effektiv. Das erzeugt viel Unzufriedenheit unter den Schülern, weil sie nicht wirklich wissen, was der PC macht. Sie kennen sich nachher mit der Mathematik nicht aus.
Je größer das Projekt ist, umso länger dauert es. Gefahr des Scheiterns und Überforderung der Schüler. In zwei bis drei Schulwochen könnte ein Projekt abgeschlossen sein.
Nicht mit Druck unterrichten, um den Zeitplan einzuhalten. Es ist besser, einen Punkt vom Projekt zu streichen.
2 DIE EVALUATION
2.1 Evaluation der Software M@th Desktop 2.0, Fragebogen 1 (Univ.-Prof. Dr. Karl Fuchs)
Im Fokus dieses Fragebogens stand die Evaluation der Software und nicht die Unterrichtsmethode.
Der Fragebogen wurde am 25.11.2004 zusammen mit Univ.-Prof. Dr. Karl Fuchs in Salzburg entwickelt.
Hier ist der Fragebogen, der am 3.12.2004 von den Schülern ausgefüllt wurde. Sie konnten 5 Kästchen von stimme ich nicht zu bis stimme ich zu ankreuzen.
- Fragen zum Normalverteilungs Notebook
a. Bieten Dir die vorbereiteten Notebooks genug Gelegenheit
(a1) zum Experimentieren (a2) zum Anstellen von Vermutungen (a3) zur Festigung und Übung von Beobachtungen und Erkenntnissen?
b. Findest Du die Movies, bei denen Zahlenwerte verändert werden und die Auswirkungen auf die Funktionskurve bzw. auf wichtige Größen wie mu oder sigma studiert werden, für einen geeigneten Weg, die Zusammenhängen zu verstehen?
- Fragen zur Gliederung und Representation im Normalverteilungs Notebook
a. Wie hilfreich sind die Formelfenster im Definitionskapitel für Dich?
b. Wie stark erinnern Dich die Erläuterungstexte zu den einzelnen Aufgaben an die Texte in einem Schulbuch?
c. Werden bei den Aufgaben immer wieder Inhalte und Techniken vorausgesetzt, die Du nicht selbstverständlich kennst und beherrschst?
d. Ist Dir die wiederholte graphische Interpretation (Dichtefunktion - Normalverteilung) hilfreich?
e. Lenken Dich die geometrischen Darstellungen der Normalverteilung eher vom Thema ab?
- Fragen zum Taschenrechnereinsatz
a. Siehst Du das Verhältnis von Rechnen per Hand und PC Anwendung für ausgewogen an?
b. Ist der zusätzliche Einsatz eines Taschenrechners für zwischenzeitliche Rechnungen bei einzelnen Aufgaben für Dich verwirrend?
- Fragen zur Normalverteilungspalette
a. Wie hilfreich sind Dir die vorbereiteten Paletten bei der Problemlösung?
b. Ist es nicht eher so, dass Paletten die dahinterstehende Mathematik zu sehr verschleiern?
c. Könntest Du die einzelnen Aufgaben auch ohne Zuhilfenahme der Paletten, also mit den puren Mathematica Funktionen lösen?
Auf Grund der Kleinheit der Klasse, 15 Schüler, läßt sich nur eine qualitative Analyse, ein Stimmungsbild der Schüler zur Normalverteilungspalette und zum Normalverteilungsnotebook skizzieren:
In der ersten Frage, wo es um die didaktische Prinzipien: Experimenieren, Argumentieren, Üben und Festigen im Normalverteilungsnotebook ging, war ein hoher Grad der Akzeptanz bei allen Parametern festzustelle. Das unterstreicht die Behauptung, dass CAS Freude an mathematischer Arbeit wecken [Fuchshab].
In der zweiten Frage, der Mehrperspektivität d.h. Frage nach den Repräsentationsformen im Notebook, fand der überwiegende Teil der Schüler die symoblische Re-präsentation als hilfreich [Bruner]
Die Frage nach dem Vergleich von Erläuterungstexten mit Texten im Schulbuch konnte von den Schülern nicht wirklich angestellt werden. Einzelne Äußerungen sprechen dafür, dass selten mit Schulbüchern gearbeitet wurde.
Die Ergebnisse sprechen ganz deutlich dafür, dass Schüler, obwohl in der Phase der symbolischen Operationen - siehe symbol. Repräsenation - noch immer stark grafische Repräsentationen einfordern.
In der dritten Frage zur Parallelität / Interferenz zweier Hilfsmittel Notebook und Standardraschenrechner, zeigt sich deutlich, dass die beiden Werkzeuge nicht als Gegensatz, sondern vielmehr als wunderbare Ergänzung angesehen werden.
In der vierten Frage zu den Paletten [Dominik],[Simonovits1] schätzen die Schüler die bequemere Form der Eingabe durch die Unterstützung von Paletten (spezielle Menüs mit einzelnen Knöpfen für spezifische Aufgaben) in besonderer Weise.
Wenige meinen, dass Paletten die dahinterstehende Mathematik versteckt d.h. Mathematik als Black Box auftritt [Buchberger]. So wie der TR die Wurzel aus 2 ausrechnet und der Algorithmus nicht offen liegt. Da die Buttons der Normalverteilungspalette die Handrechnung quasi in Häppchen aufteilt, dürfte der Schüler auch die Handrechnung nicht ganz verstanden haben.
Manche bezeichnen als Folge ihre Fähigkeit, die Aufgaben mit den 'puren Mathematica Funktionen lösen könnten, als nicht ausreichend.
Das ist ein wichtiges Statement von einigen Schülern. Offensichtlich kann man mit den Paletten das Verstehen der Mathematik mehr in den Vordergrund rücken und Mathematica mit seiner Komplexität in den Hintergrund.
2.2 Evaluation des computerunterstützen Projektunterrichts mit Projektpräsentation, Fragebogen 2 (Univ.- Prof. Dr. Bernd Thaller)
Das Ziel des Fragebogens war es, ein Stimmungsbild der Klasse zum computerunterstützen Mathematikunterricht mit MD zu skizzieren.
Am 4. März 2005 besuchte Univ.-Prof. Dr. Bernd Thaller den Projektunterricht in der 5bk. Da die Klasse nur 2 Wochenstunden Mathematik hat, gibt es eine Doppelstunde Mathematik.
Am Ende der Doppelstunde teilte er den Fragebogen aus, der ausschließlich von ihm stammt. Dann gab es ein kurzes Gespäch mit den Schülern ohne meine Anwesenheit.
Hier ist der Fragebogen.
Bitte bewerte auf einer Skala von 1 bis 5 ob die folgenden Aussagen zutreffen oder nicht zutreffen (bitte Kästchen ankreuzen)
-
Ich interessiere mich für Mathematik.
-
Ich glaube, Mathematik wird in meinem späteren Berufsleben eine größere Rolle spielen
-
Prinzipiell finde ich den computerunterstützten Unterricht gut.
-
Der Computer hilft mir, Mathematik besser zu verstehen.
-
Ich finde das Arbeiten mit Notebooks und Paletten verwirrend.
-
Ich glaube, ein guter Lehrer könnte mir Mathematik ohne Computerhilfe besser beibringen
-
Der heutige Unterricht war typisch für den computerunterstützten Unterricht bei
Professor Simonovits -
Ich habe im Internet gelegentlich schon nach anderen Lernhilfen für Mathematik gesucht
Zum Schluss: Gib Deinem Mathematik Lehrer eine Note!
Die Resultate habe ich dem Evaluationsbericht von Univ.-Prof. Dr. Bernd Thaller entnommen:
Eine kurze Erhebung des Stimmungsbildes in der Klasse per Fragebogen und Gruppengespräch ergab folgendes. Die SchülerInnen stehen der Mathematik indifferent gegenüber. Die meisten interessieren sich weder besonders für Mathematik, noch finden sie diesen Gegenstand besonders uninteressant. Stärker ausgeprägt ist die Auffassung, dass Mathematik in ihrem späteren Berufsleben wohl keine besondere Rolle spielen wird. Sie heißen den computerunterstützten Unterricht prinzipiell willkommen und bewerten ihn sehr positiv.
Zur Frage, ob der Computer nun helfe, Mathematik besser zu verstehen, haben die SchülerInnen keine ausgeprägte Meinung. Sie glauben aber eher nicht, dass ein sehr guter Lehrer ihnen Mathematik ohne Computerhilfe besser beibringen könnte. Ihrem eigenen Mathematik-Lehrer gaben sie die Note "gut". Ausserdem bestätigten sie einhellig, dass die von mir visitierte Unterrichtsstunde typisch war.
Den SchülerInnen selbst bereitet der Umgang mit dem Computer und M@th Desktop nicht die geringsten Schwierigkeiten. Sie sind auch tatsächlich schon seit mehreren Jahren den Umgang mit dem Computer gewöhnt. Früher mussten sie Mathematica Befehle direkt eingeben, das sei eher lästig gewesen, aber mit M@th Desktop und dem daraus resultierenden Arbeitsstil sind sie sehr zufrieden. Sie haben das Gefühl, damit ein gutes Werkzeug für die mathematische Problemlösung bekommen zu haben und sie glauben, es gut anwenden zu können.
Das ist ein Snapshot von der Evaluation in der 5bk Klasse. Der Evaluator nimmt die Rolle eines aufmerksamen, unauffälligen Teilnehmers im Unterricht ein.
Am 18.3.2005 präsentierten die Schüler ihr Statistikprojekt. Der Evaluator Univ.-Prof. Dr. Bernd Thaller war auch in dieser Doppelstunde anwesend [AP, CCdiSLS, CMcCG]. Er schreibt in seinem Evaluationsbericht:
Die Arbeiten wurden in Kleingruppen von je zwei SchülerInnen durchgeführt und sollten eine typische Anwendung der Normalverteilung zeigen. Die Aufgabenstellung war von den SchülerInnen selbst zu wählen. Die Problemstellung, die Theorie, und die Problemanalyse war in einem M@th Desktop Arbeitsbatt darzustellen. Die Präsentation bestätigte die positive Beurteilung der Klasse durch Herrn Dr. Simonovits.
Die Projektarbeiten wurden durchwegs mit Begeisterung und Engagement vorgetragen, die Freude an der optisch eleganten Präsentation mit Hilfe von M@th Desktop war deutlich spürbar. Die SchülerInnen wählten sich interessante und originelle Aufgabenstellungen, wie z.B. die Verteilung der Ping-Werte in Computer-Netzwerkspielen, den Zusammenhang zwischen Gesundheitsausgaben und Lebenserwartung in den einzelnen Staaten der Erde, die finanzielle Situation der Studierenden, etc. Die Analyse der Daten erfolgte mathematisch-numerisch, die Erläuterung der Resultate erfolgte vorwiegend mit Hilfe der grafischen Darstellungsmöglichkeiten, die M@th Desktop bietet.
2.3 Der Evaluationsbericht (Univ.-Prof. Dr. Bernd Thaller), Fotogallerie
Die Evaluierung des Projektes und der Software von Seiten des Univ.-Prof. Dr. Bernd Thaller ist ausführlich und spannend zu lesen. Er umfaßt knapp drei Seiten. Das ist seine Zusammenfassung:
(1) Die e-Learning Sequenzen zur Normalverteilung stellen eine nützliche und ansprechende Unterrichtshilfe dar.
(2) Der Computer ist kein Werkzeug, um Unterrichtszeit einzusparen. Die Kombination konventioneller und computerunterstützter Unterrichtsphasen erfordert eigentlich zusätzliche Unterrichtszeit.
(3) Der Wechsel der Unterrichtsformen zwischen der konventionellen und der computerunterstützten Unterrichtsform ist ein wesentliches Element des Unterrichtserfolges. Dadurch wird es möglich, denselben Lerninhalt mit Hilfe völlig verschiedener Schüleraktionen zu erarbeiten. Außerdem wird dadurch das Aufmerksamkeitsniveau und die Zufriedenheit der SchülerInnen gesteigert.
(4) Die Software ermutigt die SchülerInnen, bei der Lösung von Aufgaben symbolische, numerische, grafische und textuelle Darstellungsformen in einem ausgewogenen und dem jeweiligen Zweck angemessenem Verhältnis zu wählen.
Klicke hier, um eine genaue Beschreibung und zusätzliche Details zu lesen.
Fotogallerie: Klicke hier um die 13 Fotos vom Projektunterricht und der Evaluation zu sehen.
Eine persönliche Schlußbemerkung:
Das Projekt ist von der Klasse ganz gut aufgenommen und durchgeführt worden. Dafür habe ich mich auch bei der 5bk bedankt.
Die Matura einige Monate später haben alle Schüler der Klasse bestanden.
3 LITERATUR
[MD] Die Mathematikunterrichtssoftware M@th Desktop 2.0 (MD) beinhaltet derzeit die Module Basics, Differenziation, Integration und MDTools. Die Homepage des Produktes ist www.deltasoft.at. MDs engine ist Mathematica. Eine Demoversion von MD und Mathematica ist von Deltasoft downloadbar.
[BL1] MAYR, Peter; SEUFERT, Sabine (2002) Definition des Blended Learning im Buch Fachlexikon e-learning , http://beat.doebe.li/bibliothek/b01275.html
[BL2] BAUMANN, Thomas (2003) Definition des Blended in der Zeitschrift Lehren und Lernen mit neuen Informations- und Kommunikationstechnologien I im Text E-Learning in der Lehrerinnen- und Lehrerbildung auf Seite 52 http://beat.doebe.li/bibliothek/b01876.html
[Fuchshab] FUCHS, Karl Josef (1998): Computeralgebra - Neue Perspektiven im Mathematikunterricht. Habilitationsschrift an der Naturwissenschaftlichen Fakultät der Universität Salzburg zur Erlangung der Venia Docendi aus Didaktik der Mathematik
[Bruner] BRUNER, Jerome (1970): Der Prozeß der Erziehung. Verlag Schwann Berlin, Düsseldorf
[Buchberger] BUCHBERGER, Bruno (1989): Should Students Learn Integration Rules? Technical Report. RISC-Linz
[CCdiSLS] COBB, P., CONFREY, J., DISESSA, A., LEHRER, R., & SCHAUBLE, L. (2003): Design experiments in education research. Educational Researcher, 32 (1), 9-13.
[CMcCG] COBB, P., MCCLAIN, K., & GRAVEMEIJER, K. (2003): Learning about statistical covariation. Cognition and Instruction, 21, 1-78.
[Dominik] DOMINIK (2003): Mathematica Paletten als Lern- und Experimentiertools im Mathematisch Naturwissenschaftlichen Unterricht. Dissertation Universität Salzburg.
[Simonovits1] SIMONOVITS, Reinhard (2000): Projekt M@th Desktop. Didaktikhefte Österreichische Mathematische Gesellschaft] 32, 172-179
[Simonovits2] SIMONOVITS, Reinhard (2001): Differentialrechnung mit M@th Desktop. Didaktikhefte [Österreichische Mathematische Gesellschaft] 33, 130-139
[Simonovits3] SIMONOVITS, Reinhard (2002): EU-Projekt mit M@th Desktop, basierend auf Mathematica. Didaktikhefte [Österreichische Mathematische Gesellschaft] 34, 101-110.
[Simonovits4] SIMONOVITS, Reinhard (2003): Daten fitten und approximieren mit Mathematica und M@th Desktop. Didaktikhefte [Österreichische Mathematische Gesellschaft] 35, 98-103
[KainhoferSimonovits] KAINHOFER, Reinhold; SIMONOVITS, Reinhard (2003): M@th Desktop and MD Tools: Mathematics and Mathematica Made Easy for Students. Reinhold Kainhofer, ReinhardSimonovits, conference proceeding of PrimMath[2003], Zagreb: 123 - 138
[Simonovits5] SIMONOVITS, Reinhard (2004): Lineare Regression mit Mathematica und M@th Desktop. Didaktikhefte [Österreichische Mathematische Gesellschaft] 37, 137-154
[Führer] FÜHRER, Lutz (1997): Pädagogik des Mathematikunterrichts. Verlag vieweg, Braunschweig, Wiesbaden
[Wittmann] WITTMANN, Erich Christian (1974): Grundfragen des Mathematikunterrichts. Veralg vieweg, Braunschweig, Wiesbaden
[AP] ALTRICHTER, Hubert, POSCH Peter (1998): Lehrer erforschen ihren Unterricht. Eine Einführung in die Aktionsforschung. Verlag Klinkhardt Bad Heilbrunn
[SmoleSimonovitsThaller] SMOLE, Markus; SIMONOVITS, Reinhard THALLER, Reinhard; Bernd (2004): Messen von Radwegen mit Mathematica und M@th Desktop. MNU Jg 57,5: 271-276
[Diplomarbeit1] FINK, Rainer (2001): Auf Mathematica basierende Entwicklung von Lerneinheiten mit M@th Desktop auf dem Gebiet der Differenzialrechnung
[Diplomarbeit2] SILLER, Hans-Stefan (2002): Auf Mathematica basierende Lerneinheiten zur fundamentalen Idee der Modellbildung, illustriert an Extremwertbeispielen und Beispielen der Integralrechnung mit M@th Desktop
[Diplomarbeit3] WELIK, Werner (2002): Auf Mathematica basierende Entwicklung von Lerneinheiten zu Anwendungen der Integralrechnung unter M@th Desktop verbunden mit dem methodisch zielgerichteten Einsatz eines Help Browser-Systems
[Diplomarbeit4] SMOLE, Markus (2003): Auf Mathematica und M@th Desktop basierende Unterrichtsequenzen zur Approximation von Radwegen sowie zur linearen Regression und Korrelation
[Diplomarbeit5] ROTH, Gerald (2003): Auf Mathematica und M@th Desktop basierende Unterrichtsequenzen zur Volumsbestimmung von Rotationskörpern sowie Anwendungen des Student-t-Tests
Alle Diplomarbeiten sind unter
MDT Paletten
MDTools - Paletten Version 2.0
MDTools stellt 11 Paletten zur Verfügung.
Zu jedem Button auf der Palette gibt es ein Musterbeispiel im Helpbrowser.
Was kann damit gemacht werden?
Die Plot Palette plottet 2D und 3D Funktionen
"2DPlots" bietet die Buttons für Plot, ImplicitPlot, ParameterPlot, ListPlot.
"3DPlots" bietet die Buttons für Plot, Kurven, Oberflächen, Kontouren, Dichtedarstellungen.
Die "Helper Palette PlotOptions" lässt die wichtigsten Optionen komfortabel einfügen
(klicken Sie auf die Palette, um sie zu vergrößern.)
Die Algebra Palette formt Polynome und Trig. Terme um
"Polynome" bietet die Buttons für Expand, Factor, Simplify, FullSimplify, Together, Apart, PowerExpand.
"Komplex" bietet die Buttons für ComplexExpand.
"Trigonometrie" bietet die Buttons für TrigExpand, TrigFactor.
Die "Helper Palette" mehr bietet zusätzliche Funktionen an.
(klicken Sie auf die Palette, um sie zu vergrößern.)
Die Lineare Algebra Palette arbeitet mit Vektoren, Matrizen und Gleichungsystemen
"Matrizen" bietet die Buttons für Matrizenmultiplikation, Skalar*Matrix, Determinanten, Inverse, Eigensystem, Einheitsmatrix, Transponierte, Komplex Konjugierte Matrix.
"Gleichungen lösen" bietet die Buttons für Solve NSolve.
"Vektoren bietet" die Buttons für Skalarprodukt, Kreuzprodukt, Länge, Matrix * Vektor, Skalar * Vektor.
(klicken Sie auf die Palette, um sie zu vergrößern.)
Die Differenziation Palette differenziert, bildet Divergenz, Gradient und Rotor, berechnet Taylorreihen und Limits
"Eine Variable" bietet die Buttons für das Differenzieren mit einer Variablen.
"Mehrere Variablen" bietet die Buttons für das Differenzieren, totales Differenzial, Divergenz, Gradient, Rotor.
"Taylor Reihen" bietet die Buttons für Reihenbildung, Koeffizienten, O[n] und Plot.
"Limit" bietet die Buttons für Limes und numerische Limesberechnung
(klicken Sie auf die Palette, um sie zu vergrößern.)
Die IntegrationsPalette löst Integrale, Diff. Gleichungen und bildet Fourierkoeffizienten
"Integrale" bietet die Buttons für Unbestimmtes Integral, Bestimmtes Integral, Numerischer Wert, Integrieren mit mehreren Variablen.
"Diff Gleichungen" bietet die Buttons für DSolve, NDSolve, Solve & Plot.
"Fourier Reihen" bietet die Buttons für an, bn und cn
(klicken Sie auf die Palette, um sie zu vergrößern.)
Die Data Fitting Palette importiert, visualisiert und fitted Daten
"Daten importieren" bietet die Buttons Daten einlesen und FilePath.
"Plot Daten" bietet die Buttons für xi, yi; yi; und xi,yi mit erri Darstellung.
"Least square" bietet die Buttons für Fitte Daten, Plot Resultat mit Daten, Plotte
"Nicht lineare Modelle" bietet die Buttons für NonLinearFit
(klicken Sie auf die Palette, um sie zu vergrößern.)
Die Normalverteilung Palette berechnet Normalverteilungswerte, Konfidenzintervalle und Hypothesentests
"Daten und z Tools" bietet die buttons x,s; Phi[z], z[Phi].
Normalverteilung bietet die buttons X<=Value, Value <=X, Value <= X <= Value, a,b?, n?
"Konfidenzintervall" bietet die Buttons [Mu], xSampleSize?, [p], pSampleSize?
"Hypothesentest" bietet die Buttons für H1<, H1>, H1 =!=
(klicken Sie auf die Palette, um sie zu vergrößern.)
Die Student t Chi F Test Palette arbeitet mit dem Student t Tes, Chi^2 Test und F Test
"Student t Test, gepaarte Daten" bietet die Buttons Mu1 > Mu2, Mu1 =!= Mu2
"Student t Test, unabhängige Daten" bietet die Buttons Mu1 > Mu2, Mu1 =!= Mu2
"Chi^2 Test" bietet die Button Kontingenztabelle und Fit
"F Test" bietet die Buttons Sigma1 > Sigma2, Sigma1 =!= Sigma2
(klicken Sie auf die Palette, um sie zu vergrößern.)
Die Krypto-Mathematik Palette arbeitet mit Restklassen und Verschiebechiffren
Arithmetik" bietet grundlegende Funktionen für die Arbeit mit ganzen Zahlen, wie den ggT, kgV, Integer-Faktorisierung und den Euclidschen Algorithmus.
"Restklassen" erzeugt Restklassen, bildet Inverse in Restklassengruppen, bietet die Eulersche Phi-Funktion, schnelle modulare Exponentiation, berechnet Primitivwurzeln und diskrete Logarithmen.
"Verschiebechiffren" bietet Funktionen zum Ver- und Entschlüsseln eines Textes durch verschieben der Zeichen im Alphabet und eine Analyse-Funktion zur Bestimmung des Schlüssels aus einem verschlüsselten Text.
(klicken Sie auf die Palette, um sie zu vergrößern.)
Die Krypto-Systeme Palette stellt Verschlüsselungssysteme und ein Schlüsselaustauschverfahren zur Verfügung
"RSA" implementiert den Public-Key Algorithmus RSA und bietet eine Funktion um den privaten Schlüssel zu ermitteln.
"Diffie - Hellman" implementiert einen Schlüsselaustausch über eine öffentliche Leitung nach dem Diffie-Hellman Algorithmus.
"ElGamal" implementiert den Public-Key Algorithmus ElGamal und bietet eine Funktion um den privaten Schlüssel zu ermitteln.
(klicken Sie auf die Palette, um sie zu vergrößern.)
Die Krypto-Signaturen Palette stellt eine Hashfunktion und Signatur-Algorithmen zur Verfügung.
"Hashfunktionen" bietet die Hashfunktion SHA-1.
"RSA - Signatur" Erstellt und Verifiziert eine RSA-Signatur.
"ElGamal - Signatur" Erstellt und verifziert eine ElGamal-Signatur.
"DSA-Signatur" Verwendet den Digital Signature Algorithmus zum erstellen und verifizieren einer Signatur.
(klicken Sie auf die Palette, um sie zu vergrößern.)
MDT Arbeitsblatt
MDTools - Arbeitsblatt
Das Arbeitsblatt in MDTools dient dazu, kleine Vorlesungsskripten und Übungsbeispiele zu erstellen. Das geschieht durch Professoren als auch Studenten.
Standardmäßig sind 3 Skripten für Studenten in MDTools enthalten:
-
Analysisbeispiele mit MDTools
-
Kryptographie mit MDTools
-
Typische Anwendungsbeispiele mit MDTools
Das Kryptographie Notebook führt in die mathematischen Grundlagen und den Umgang mit kryptographischen Funktionen ein. Darin wird auch die Verwendung der Paletten ausführlich demonstriert.
ein MDTools Arbeitsblatt
(Klicken Sie auf das Arbeitsblatt um es zu vergrößern.)
Strukturierbares Lerngebiet
- Titel
- Abschnitt
- ansprechendes Design
Vordefinierte Styles
- Answer
- Example
- Exercise
- Formula
- Internet
- Summary
- daVinciRed
- PicassoGreen
- WarholOrange
- vanGoghBlue
- RaffaelGreen
- Instruction
- Solution
Starthilfe
- Tip of the Day
- Link zum Helpbrowser
FAQ
MD Tools
Mathematica 3.0 crasht, wenn ich MDTools mit F7 starten möchte.
MDTools startet nicht, wenn ich F7 presse. (Mathematica 4.0 und 4.1)
Mathematica 4.1 crasht, wenn ich die Cell Styles "Answer", "Excercise", "Internet" etc, des MDTools Notebooks benütze.
- Mathematica 3.0 crasht, wenn ich MDTools mit F7 starten möchte.
Das passiert, wenn nur die Menüleiste von Mathematica am Bildschirm ist und kein Fenster offen ist. Das ist zum Beispiel der Fall, wenn nach dem Starten von Mathematica das Notebook Untitled-1.nb geschlossen wird:
Lösung: (1) Menüleiste File > New drücken, (2) MDTools starten.
- MDTools startet nicht, wenn ich F7 presse. (Mathematica 4.0 und 4.1)
Lösung: Wenn mit MDTools gestartet wird, muss zumindest ein leeres oder beschriebenes Notebook geöffnet sein.
- Mathematica 4.1 crasht, wenn ich die Cell Styles "Answer", "Excercise", "Internet" etc, des MDTools Notebooks benütze.
Ich vewende mehrere Cell Styles, die im MDTools Notebook verfügbar sind. Sobald ich versuche, irgendwas in eine Zelle des Styles "Answer", "Excercise", "Internet", "Formula" etc, zu schreiben, stürzt das Mathematica Front End und der Kernel ab.
Lösung: Wegen eines bugs im Mathematica 4.1.0. Front End können diese Cell Styles des MDTools Notebooks nur verwendet werden, wenn
(1) zuerst eine Textzelle erzeugt wird und in diese ein Leerzeichen eingegeben wird.
(2) die Zellenklammer dieser Textzelle markiert wird
(3) in der Stylebox "Answer", "Excercise", "Internet", "Formula" etc ausgewählt wird.
Jetzt liegt das gewünschte Zellformat vor.